The
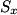 operator in matrix form is given by operator in matrix form is given by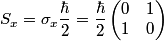 An eigenspinor of 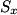 with eigenvalue with eigenvalue 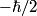 must satisfy must satisfy  We can convert all of the answers to vector notation by using the identifications 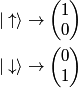 We can then check whether the condition in equation (1) is satisfied. We find that it is satisfied only for answer (C). Therefore, answer (C) is correct. Physically, this means that the eigenspinor in answer (C) represents a particle with definite  -component of its spin vector equal to -component of its spin vector equal to 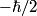 . . |